Candium & Pennium Labs

Candium Lab

Purpose:

• To use a Candium model to explain the concept of atomic mass.
• To analyze the isotopes of Candium and calculate its atomic mass.

Hypothesis: We hypothesized that the Gobstoppers would have a higher atomic mass and the Sixlets would have the lowest atomic mass because of their sizes.

Materials:

• 4 Sample of Candium
• Triple Beam Balance

Procedure:

1. Obtain 4 samples of Candium
2. Separate it into its 4 isotopes (M&M's, Skittles, Sixlets, & Gobstoppers)
3. Determine the total mass of each isotope.
4. Count the number of each isotope.
5. Record data and calculations in the data table.
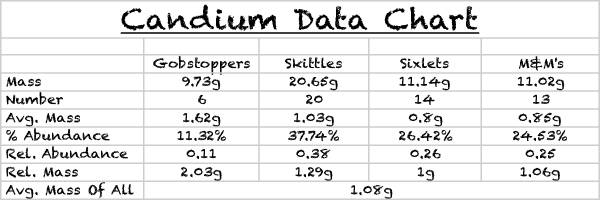
   Create a data table that has the following:
   1. Average mass of each isotope
   2. Percent abundance of each isotope
   3. Relative mass of each isotope
   4. Relative abundance of each isotope
   5. Average mass of all isotopes
       Your data table should have five columns and seven rows.

A mix of the samples on the triple beam balance

Discussion: In this lab, we gathered a bag of miscellaneous samples of candium and we first sorted out the four samples before moving on. We then brought a triple beam balance to our work station and started weighing each sample and calculated the mass to the nearest hundredth decimal point. Then we used the equations that we were given and calculated the rest of the data to complete the data table.

Isotope- One of two or more atoms having the same atomic number but different mass numbers.


Relative abundance is a comparison between the isotopes and percent abundance is comparing the totals.

The errors that could of happened was we could have done the calculations wrong or we could have counted the samples wrong and all the data would've of been wrong.

Conclusion: We have accepted our hypothesis because the atomic mass of the Gobstoppers was 1.62g, which was much larger than any of the other samples of candy.

Pennium Lab

Purpose: To investigate the concept of atmoic mass and how it was derived. You will develop your own unit of measure CMU (coin mass unit) and use it to measure relative masses of other coins.

Materials:
 1. A packet of pennies.
 2. 1 quarter, nickel, dime

Procedure:

1. Obtain a packet of pennies.
2. Sort the pennies into two groups: pre 1982 and post 1982.
3. Measure the mass (in grams) of each stack of pennies. Record the masses in a data table
4. Count the number of pennies in each stack.
5. Measure the mass in grams of a quarter, nickel, and dime. Record these values in the data table.
6. Determine the average mass of pre-1982 pennies. 3.05grams
7. Determine the average mass of post-1982 pennies.  2.46grams
8. Choose one of your coins to make CMU. Let's say that the mass of a nickel is one CMU.  Use the mass of a nickel to calculate the mass of a quarter, nickel dime, pre and post 1982 pennies. (make sure you always record your data).
9. Determine the average mass.

Questions:

1. Does each penny have the same mass?  No they all have different masses.
2. Can you identify two penny isotopes based on the masses of the pennies?  Pre 1982 and post 1982 because their mass values are different so they were most likely made with different elements.
3. What does your data tell you about the relationship between mass of a penny and date of a penny?  It tells us that the compostition consisted of different materials.

Discussion:
The average mass of the pre and post pennies is 25.97 grams.
My weight in CMUs is 22049995.28 CMU
How I calculated that was took the Nickel which CMU is 1 and it weighed  4.72 so I calculated my weight into kg which I weighed 100lbs. then I converted that to grams then subtracted 4.72 from that number and got my answer.

Conclusion:
We decided to use the Nickel as the CMU which meant that a CMU weight would be 4.72 grams. The mass of a quarter was 5.46 grams so we took the CMU and subtracted it from that and got our answer of 1.16 CMUs.
Using the idea of the CMU we can come up with a conclusion of how scientist figured out the atomic mass unit. They probably took the most common measurement of atoms and set that as the Atomic mass unit then that would be the bases of every measurement.

Aluminum Foil

Purpose:  To become familiar to with the laboratory and to make qualitative and quantitative observations about physical and chemical changes during a chemical reaction.


Question:  What will happen when you put in aluminum foil with CUSO4 (Water mixed with copper(2) sulfate pentahydrate)?  Will it be a chemical or physical change when you add NaCl (sodium chloride)?


Hypothesis: When we add the ball of aluminum foil into the liquid with copper sulfate pentahydrate and without the salt added, there will be a chemical change, but there will be a bigger chemical change when the salt is added to the solution.




Materials:  

• Beaker (150 or 250 ml)
• Copper (2) sulfate pentahydrate - use caution
• Toxic substance scoopula
• 100 ml graduated cylinder
• Stirring rod 
• Thermometer
• Small square of aluminum foil

Procedure:

1. Grab a beaker, 100mL graduated cylinder, a scoopula, a thermometer, a small square of aluminum foil.
2. Measure 75-100mL of water in your graduated cylinder and pour into beaker. The exact amount is not important in this lab.
3. Using a scoopula, gather some copper(2) sulfate pentahydrate. Again the amount is not important, but feel the scoopula about one quarter full. Place the copper(2) sulfate pentahydrate in the beaker. Use stirring rod until all the solids are dissolved into the liquid.
4. Obtain your piece of aluminum foil and crumple it into a loss ball. Place the aluminum foil ball into the liquid. Stir gently for 15 seconds.
5. Make sure your scoopula is clean and obtain a large scoop of sodium chloride for the labeled container and add it to the solution. Stir until dissolved.
6. After observing, let stand for 10 minutes then dispose of the solution in the specified area. Clean materials thoroughly with soap and water and make sure your lab area is fully cleaned.

Data:

Mixing the copper sulfate pentahydrate thoroughly into the water!

The copper sulfate pentahydrate made the water turn a blueish color.

When we added the salt to the beaker, the aluminum foil produced bubbles

on the part that was in the liquid.

After stirring the mixture and letting the chemicals react, it produced copper rust but it wasn't actually copper, but was the copper sulfate being taken off of the aluminum ball!

But it was a pretty red color!

Discussion:  In the beginning we thought there was going to be a huge chemical change when you put in the aluminum ball into the mixture. But nothing happened until you put the salt into into the mixture then a chemical change occurred. We know a chemical change took place because  bubbles formed when no heat was added and a precipitate formed also.

Conclusion:  We have accepted our hypothesis. In conclusion, a chemical reaction took place between copper ion and aluminum, which produced a copper metal, hydrogen gas, and aluminum ions.  A chemical reaction took place because there was an increase in temperature, formation of a precipitate, and a change in color.  These are all indicators of a chemical change.

Bubble Lab!

Introduction:

Would the salt and sugar cause the bubbles to be different than the normal mixture?

A soap bubble is a very thin film of soapy water that forms a sphere with an iridescent surface. Soap bubbles usually last for only a few moments before bursting, either on their own or on contact with another object.

Hypothesis:

The sugar bubble will pertain a different color than the regular bubble and salt bubble. The salt bubble will have a clear effect to it and have no rainbow inside it.

Materials:

3 Drinking cups

1 tsp. of liquid dish detergent

1/2 tsp. of table sugar

1/2 tsp. of table salt

3 straws

1 spoon

2/3 cup of water to go in each cup

Procedures:

1. Label  3 drinking cups 1,2, and 3 and measure and add 1 tsp. of liquid dish detergent to each cup. Use measuring cup to add 2/3 of a cup of water then swirl the cups with a spoon to form a clear mixture.

2. Add 1/2 tsp. of table sugar to cup 2 and 1/2 tsp. of table salt to cup 3. Swirl each cup for a minute.

3. Dip the straw into cup one and remove it and blow gently into the straw to make large bubbles. Practice your bubble blowing.

4. Repeat step 3 with the mixtures in cups 2 and 3.

Data:

The normal mixture bubble  (teacher approved)

The sugar bubble 

The salt mixture would not form a bubble.

In doing this experiment we realized many errors could have occurred like the mixture could be different from what they should be because we used a spoon instead of an actual measuring cup.  Also different people were blowing bubbles which could change the consistency of the bubbles being formed.

Discussion:

The normal bubble would form a bubble then fall off of the straw and pop.

The sugar bubble would stick to the straw and you would have to touch it in order for in to be popped. 

The salt mixture did not blow bubbles.

Conclusion:

We reject our hypothesis because it had nothing to do with the color, but it dealt with how long the bubble would last.  The Reason that the soap mixture with sugar lasted longer is because how long a bubble lasts depends on how quickly the surface dries. Glycerin slows down the drying process and that's exactly what sugar is made out of. It allowed the surface to stay wet longer and not dry as quickly.  The salt mixture wouldn't allow a bubble to form because as soon as you tried to blow a bubble the surface would dry very quickly and just pop.